On the Abuse of Exponentiation in Colloquial Communication
Or, to put it another way, “Why I Hate it When People Say Things ‘Grow Exponentially.’” But hey, why say something simply when you can say it in polysyllables? In any case, something which I have been finding increasingly irksome is when people talk about something “growing exponentially,” when all that they really mean is that it is growing really quickly. I guess I shouldn’t really blame them for this, seeing as it’s more the lousy math education standards which are to blame. But still, I do wish that they could get this in their heads: just because it’s growing quickly doesn’t mean that it’s growing exponentially!
 Let
me back up a bit. For those of you with a bit of mathematical or scientific
background this will be review, but I’ll include it in case of the unlikely even
that there is anyone here without a second year university calculus class under
their belt. And, given how nerdy/awesome my friends are, that is rather unlikely.
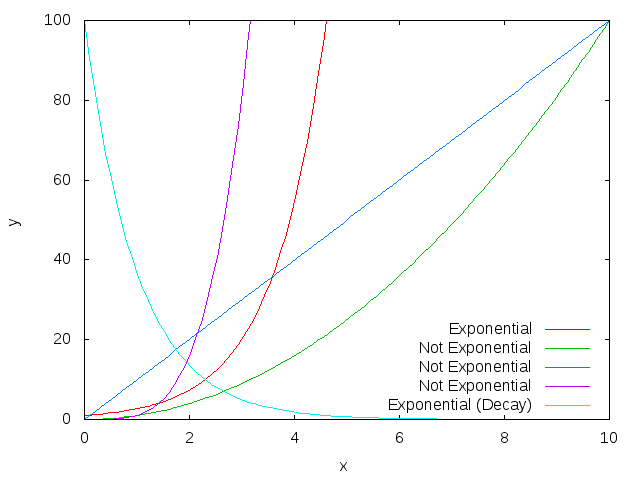
Exponential
growth refers to something that, over some fixed interval, will increase in size by
some constant factor. For example, if the water in my sink is getting higher
exponentially, that means it starts off at, say, 1cm deep. After a minute it is
2cm deep. After another minute it is 4cm deep. After another minute it is 8cm deep.
Pretty soon my whole apartment will be full of water, the landlord will be
asking some difficult questions, and I’ll be wishing that I’d chosen a drier example
with which to make my point.
Let
me back up a bit. For those of you with a bit of mathematical or scientific
background this will be review, but I’ll include it in case of the unlikely even
that there is anyone here without a second year university calculus class under
their belt. And, given how nerdy/awesome my friends are, that is rather unlikely.
Exponential
growth refers to something that, over some fixed interval, will increase in size by
some constant factor. For example, if the water in my sink is getting higher
exponentially, that means it starts off at, say, 1cm deep. After a minute it is
2cm deep. After another minute it is 4cm deep. After another minute it is 8cm deep.
Pretty soon my whole apartment will be full of water, the landlord will be
asking some difficult questions, and I’ll be wishing that I’d chosen a drier example
with which to make my point.
A related concept is exponential decay. This is essentially the same thing, except here the quantity decreases by some constant factor. For example, say I have a chocolate bar with eight segments and in the first minute I eat half of it (four pieces). Wanting to savour it, over the next minute I eat half of the remaining chocolate, or two pieces. Wanting to stretch out my chocolate still longer, the next minute I eat only 1 piece. The next minute I eat only half a piece. This process continues and I never actually finish the chocolate bar. Of course, this example is totally unrealistic: in reality I would have eaten the whole chocolate bar within the first minute.
The thing is, the never-quite-vanishing chocolate bar exhibits exponential behaviour, while most things that people call exponential do not. The thing about exponential growth is that it tends to explode; it will eventually start growing so quickly that it just can’t continue. Take population growth, for example. Populations are often thought of as growing exponentially. But this can not last forever. Eventually there won’t be enough food and the population will level off.
Whenever I see something referred to as “increasing exponentially,” my immediate reaction is to ask for a plot of the data or the chi-squared value for an exponential fit. For reasons that I explained above, it is almost certainly not growing exponentially. It might be growing quickly, but that is not at all the same thing. So please, spare us neurotic math-geeks a bit of unnecessary squirming and describe the trend properly.
comments powered by Disqus
